3 - Linked List Implementation II - 2101637541 - Vick Koesoemo Santoso
3 - Linked List Implementation II - 2101637541 - Vick Koesoemo Santoso
Stack Concept
Stack merupakan data struktur
yang penting yang menyimpan elementnya secara teratur.
Analogi :
Seperti tumpukan piring dimana
jika kita ingin mengambil piring maka kita harus mengambilnya dari yang paling
atas.
Ø Stack
adalah linear data struktur yang bisa diimplementasikan dengan array atau
linked list
Ø Element
dalam stack bisa ditambah atau dikurangkan dari data yang paling akhir yang
biasa disebut “Top”
Ø Data
tersebut disimpan dalam konsep (LIFO) Last In First Out.
Array
Representation
Stack punya 2 variable :
Ø TOP
digunakan untuk menyimpan alamat element paling atas dari Stack
Ø MAX
digunakan untuk menyimpan data maksimal yang bisa ditampung oleh Stack
Ø Jika
TOP = NULL maka data dalam Stack kosong
Ø Jika
TOP = Max-1, maka data dalam Stack penuh
Yang membedakan Array dengan Linked list , didalam array
kita harus memesan terlebih dahulu memory box untuk menyimpan datanya. Jika
memory box penuh maka data sudah tidak dapat ditambahkan tetapi dalam linked
list kita tidak perlu memesan memory boxnya kita hanya memesan jika kita ingin
menambahkan data.
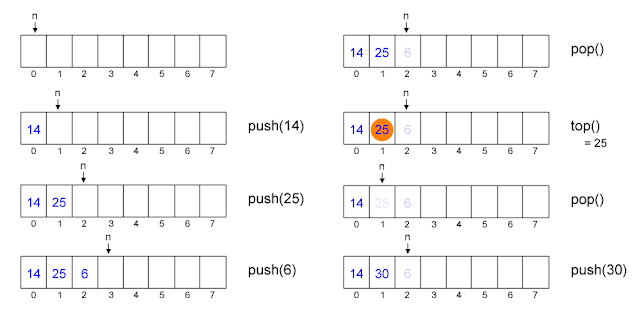
Stack
Operations
Push(x) :
Menambahkan data x ke paling atas stack
Pop() :
Mengapus data dari data paling atas stack
Top() :
Memgembalikan data ke data paling atas stack
Infix, Postfix, and Prefix Notation
Ada 3 notasi aritmatika yang
diketahui :
Ø Prefix
notasi (Reverse Polish notation)
Ø Postfix
notasi (Polish notation)
Ø Infix
notasi
Notasi
postfix diberikan oleh Jan Lukasiewicz yang adalah seorang Polandia
ahli
logika, matematikawan, dan filsuf. Tujuannya adalah untuk berkembang
Notasi
awalan bebas tanda kurung (juga dikenal sebagai notasi Polandia)
dan
notasi postfix yang lebih dikenal dengan Reverse Polish
Notasi
atau RPN.
Ø Prefix :
operator ditulis sebelum operands
Ø Infix : operator ditulis antara
operands
Ø Postfix : operator ditulis setelah operands
DFS(Depth
First Search)
(DFS)
adalah algoritma untuk melintasi atau mencari
di
pohon atau grafik Kita mulai dari akar pohon (atau beberapa yang
sewenang-wenang
simpul
dalam grafik) dan jelajahi sejauh mungkin di sepanjang cabang sebelumnya
mundur.
DFS
memiliki banyak aplikasi, seperti:
Menemukan
titik artikulasi dan jembatan dalam grafik
Menemukan
komponen yang terhubung
Penyortiran
topologi
dll.
DFS
dapat diimplementasikan dengan fungsi rekursif atau iteratif
prosedur
menggunakan stack, hasil mereka mungkin memiliki sedikit perbedaan
perintah
kunjungan tapi keduanya benar.
Algoritma:
Siapkan
Stack kosong
Dorong
sumber / akar ke dalam tumpukan
Tandai
sumber / akar
Ketika
Stack tidak kosong
Pop
item dari tumpukan ke P
Untuk
setiap simpul X berdekatan dengan P
Jika
X tidak ditandai
Tandai
X
Push
X ke stack
Queue
Queue merupakan data struktur
yang penting yang menyimpan elementnya secara teratur.
Analogi :
Seperti antiran baris : Orang
yang pertama megantri maka dia yang keluar duluan.
Ø Element
dalam Queue ditambahkan di salah satu ujung yang disebut “rear” dan di hapus di
salah satu ujung lainnya yang disebut “front”
Ø Data
tersebut disimpan dalam konsep (FIFO)First In First Out.
Breadth
First Search
(BFS)
seperti DFS juga merupakan algoritma untuk
melintasi
atau mencari di pohon atau grafik.
Kita
mulai dari akar pohon (atau beberapa simpul acak di grafik) dan jelajahi semua
level node tetangga per level sampai kita menemukan tujuannya.
BFS
memiliki banyak aplikasi, seperti:
· Menemukan
komponen yang terhubung dalam grafik.
· Menemukan
jalur terpendek dalam grafik tanpa bobot.
· Metode
Ford-Fulkerson untuk menghitung arus maksimum.
Perbedaan
antara DFS dan BFS iteratif
Implementasi
hanyalah struktur data yang digunakan.
DFS
menggunakan stack sementara BFS menggunakan queue.



Komentar
Posting Komentar