4 - Introduction to Tree, Binary Tree And Expression Tree - 2101637541 - Vick Koesoemo Santoso

4 - Introduction to Tree, Binary Tree And Expression Tree - 2101637541 - Vick Koesoemo Santoso 

Tree Concept

Tree adalah Kumpulan kumpulan dari satu atau lebih nodes.

·       Node yang diatas disebut root.

·       Garis yang menghubungkan parent dengan childnya disebut edge.

·       Node yang tidak mempunyai children disebut leaf.

·       Nodes yang mempunyai parent yang sama disebut sibling.

·       Degree adalah total subtree dari node.

·       Height/Depth adalah maksimal degree dari nodes dalam sebuah tree.

·       Jika ada garis yang menghubungkan a dengan b, maka a disebut ancestor dari b, dan b disebut descendant dari a.

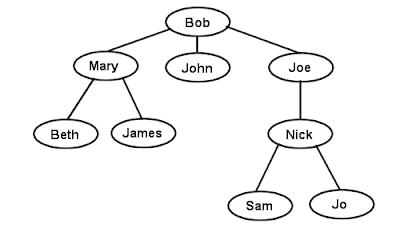
Degree dari Tree = 4

Degree dari Nick = 3

Height = 4

Parent dari John = Bob

Children dari Bob = Mary, John, Joe

Sibling dari Sama = Jo

Ancestor dari Nick = Joe dan Bob

Descendant dari Mary = Beth dan James

Binary Tree Concept

·       Binary tree adalah struktur data pohon berakar di mana setiap node memiliki paling banyak dua children.

·       Kedua children itu biasanya dibedakan sebagai left child dan right child.

·       Node yang tidak mempunyai child disebut leaf.

Contoh dari binary tree dari 9 nodes, Berakar di node yang membuat Bob.

Leaves adalah node yang memuat Beth, James, John, Sam dan Jo.

Type of Binary Tree

•        PERFECT binary tree adalah binary tree yang mana setiap tingkatnya mempunyai kedalaman yang sama.

•        COMPLETE binary tree adalah binary tree di mana setiap tingkat, kecuali yang terakhir, terisi penuh, dan semua nodes sejauh mungkin dibiarkan. Complete binary tree adalah binary tree yang lengkap.

•        SKEWED binary tree adalah sebuah binary tree dimana setiap nodenya setidaknya mempunyai satu child.

•        BALANCED binary tree adalah binary tree di mana tidak ada leaf yang jauh lebih jauh dari root daripada leaf lainnya (skema penyeimbang yang berbeda memungkinkan definisi yang berbeda "jauh lebih jauh").

Property of Binary Tree

Maksimum jumlah dari nodes di tingkat X dari sebuah binary tree adalah 2^k.

Maksimum total nodes di binary tree dari height h adalah 2^k+1 – 1.

Berdasarkan gambar diatas maka total nodesnya adalah :

= 2⁰ + 2¹ + 2² + 2³

= 2⁴ – 1

= 15

Minimal height dari sebuah binary tree dari n nodes adalah ²log(n).

Maximal height dari sebuah binary tree dari n nodes adalah n - 1.

Representation of Binary Tree

•        Implementasi menggunakan array

Index di araay mewakili nomor node.

Index 0 adalah Root node

Index kiri Child adalah 2p + 1, dimana p adalah parent index

Index kanan Child adalah 2p + 2

Index Parent adalah (p-1)/2

•        Implementation using linked list

struct data {

          int data;

          struct data *left;

          struct data *right;

          struct data *parent;

};

struct data *root = NULL;

Expression Tree Concept

Kita akan menggunakan struktur ini untuk setiap node di tree:

struct data {

          char chr;

          struct data *left;

          struct data *right;
};

ini adalah sebuah binary tree.

Prefix Traversal

menggunakan sebuah prefix atau postfix traversal di sebuah expression tree sangat sederhana.

void prefix(struct data *curr) {

          printf( “%c “, curr->chr );

          if ( curr->left  != 0 ) prefix(curr->left);

          if ( curr->right != 0 ) prefix(curr->right);
}

Di prefix,kita harus mencetak/memproses sebelum child diproses.

Postfix Traversal

void postfix(struct data *curr) {

          if ( curr->left  != 0 ) postfix(curr->left);

          if ( curr->right != 0 ) postfix(curr->right);
          printf( “%c“, curr->chr );

}

di postfix,kita harus mencetak/memproses setelah child sudah di proses.

Infix Traversal

Prefix            : *+abc

Postfix          : ab+c*

Infix salah     : a+b*c

Infix benar    : (a+b)*c

void infix(data *curr) {

          if ( is_operator(curr->chr) ) putchar( '(' );

          if ( curr->left != 0 ) infix(curr->left);

          printf( "%c", curr->chr );

          if ( curr->right != 0 ) infix(curr->right);

          if ( is_operator(curr->chr) ) putchar( ')' );

}

Vick Koesoemo Santoso

2101637541